Linear Least Squares (LLS) Method
Since there are so many more columns of ![]() than rows, the linear system is under-determined and gives rise to an
than rows, the linear system is under-determined and gives rise to an ![]() dimensional subspace (33-dimensional in our case) of reflectance curves for a single sRGB triplet. There are well-established techniques for solving under-determined linear systems. The most common method goes by various names: the linear least squares method, the pseudo-inverse, the least-squares inverse, the Moore-Penrose inverse, and even the “Fundamental Color Space” fundamental metamer.
dimensional subspace (33-dimensional in our case) of reflectance curves for a single sRGB triplet. There are well-established techniques for solving under-determined linear systems. The most common method goes by various names: the linear least squares method, the pseudo-inverse, the least-squares inverse, the Moore-Penrose inverse, and even the “Fundamental Color Space” fundamental metamer.
Suppose we pose this optimization problem:
![]()
This linearly constrained minimization can be solved easily by forming the Lagrangian function
![]()
The solution can be found by finding a stationary point of ![]() , i.e., setting partial derivatives with respect to
, i.e., setting partial derivatives with respect to ![]() and
and ![]() equal to zero:
equal to zero:
![]()
Solving this system by eliminating ![]() gives the LLS solution
gives the LLS solution
![]()
Thus, a reflectance curve can be found from a sRGB triplet by simply converting it to linear ![]() and multiplying it by a 3
and multiplying it by a 3![]() 3 matrix,
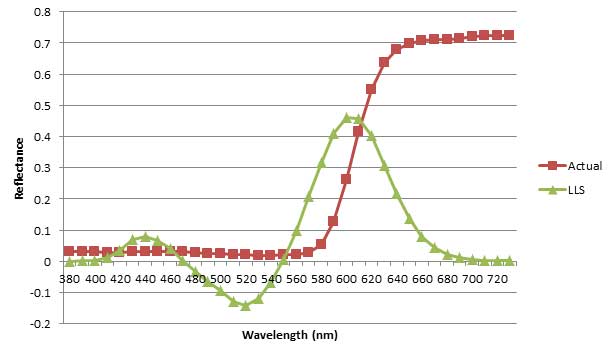
3 matrix, ![]() . Unfortunately, the resulting solution is sometimes not very useful. Consider its application to this reflectance curve, which represents a bright red object color:
. Unfortunately, the resulting solution is sometimes not very useful. Consider its application to this reflectance curve, which represents a bright red object color:
The LLS solution contains negative reflectance values, which don’t have physical meaning and limit its usefulness in realistic applications. Computationally, this is a very efficient method. The matrix ![]() can be computed in advance, as shown here, and each new sRGB value needs only be multiplied by it to get a reflectance curve.
can be computed in advance, as shown here, and each new sRGB value needs only be multiplied by it to get a reflectance curve.
Navigation
The presentation is spread over several web pages. Click the Next Page or Previous Page links to move sequentially. To access a page directly, use these links:
1. Introduction
2. Computing an sRGB triplet from a Reflectance Curve
3. Linear Least Squares (LLS) Method (this page)
4. Least Slope Squared (LSS) Method
5. Least Log Slope Squared (LLSS) Method
6. Iterative Least Log Slope Squared (ILLSS) Method
7. Iterative Least Slope Squared (ILSS) Method
8. Comparison of Methods
9. Conclusions (pre-6/4/19)
10. Update 6/4/19: Least Hyperbolic Tangent Slope Squared (LHTSS) Method