Subtractive Color Mixture Computation (Page 3)

Subtractive Mixture of Two Reflectance Curves

Suppose we have the reflectance curves for two colors we wish to mix subtractively. After researching the web for insight into this, I found that multiplying the reflectance curves together is a step in the right direction, but will mimic a special type of subtractive mix that results from passing white light through two colored filters, assuming the filters have transmittance curves matching the reflectance curves of two colored objects.

But I’m more interested in modeling how paints mix instead of how colored filters act. In the case of two colored objects, I found a website by Bruce MacEvoy called handprint.com that suggests that the “geometric mean” of the two reflectance curves will give a reasonable prediction for the mixture of two watercolor paints in equal proportion. The geometric mean of two reflectances would be computed by multiplying them together, element by element, and then taking the square root of each product. I decided to investigate further this model of subtractive mixture.

One thing the handprint web site did not address is how to mix colors in unequal proportions, say, five parts of one color to two parts of another. Here, the “weighted geometric mean” is useful. (This idea arose from my previous work in Geometric Programming and the Monomial Method.) If we define the weights, $\delta$ , to be the fraction of the total that each color contributes to the mix, then the weighted geometric mean (WGM) is

$\rho_{mix} = \rho_1^{\delta_1}\;\rho_2^{\delta_2}.$

For example, if we want five parts of the first color and two parts of the second, we would use $\delta_1=5/7$ and $\delta_2=2/7$ . We would then multiply the two reflectance curves together after raising each value in them to the $\delta$ power. Can you see how the case of equal parts of two colors simplifies to the square root of the product of the reflectances?

This extends easily to a mix of more than two colors. Each reflectance curve gets raised to the fraction that it contributes to the whole. A 4:5:6 mix of three colors would be

$\rho_{mix} = \rho_1^{4/15}\;\rho_2^{1/3}\;\rho_3^{2/5}.$

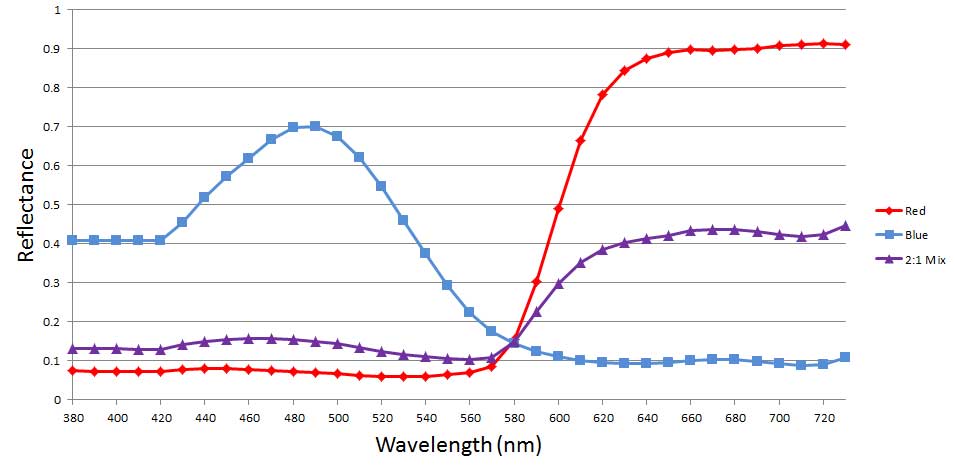
As an example, suppose we have two reflectance curves representing a red paint and a blue paint. The graph below shows the mix reflectance coming from a 2:1 mix of red and blue, $\rho_r^{2/3}\;\rho_b^{1/3}$ :

2:1 mixture of red and blue by the weighted geometric mean.

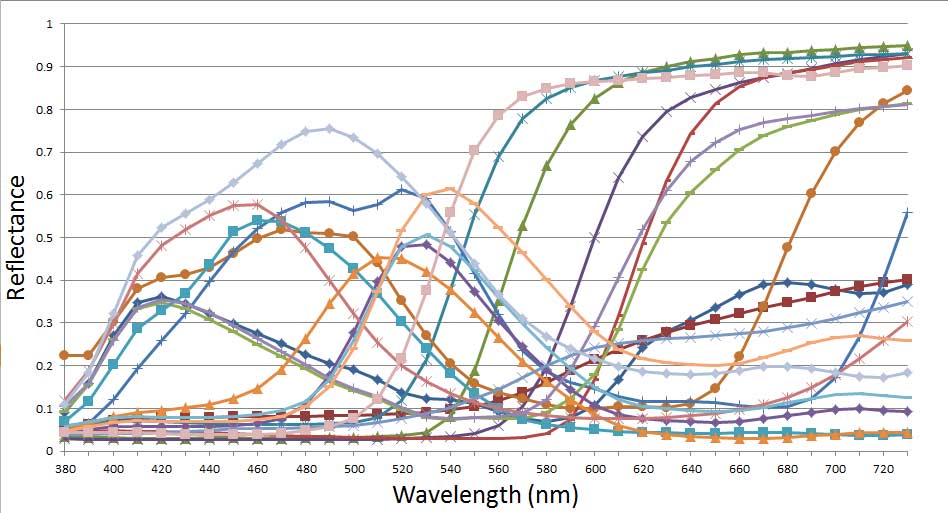
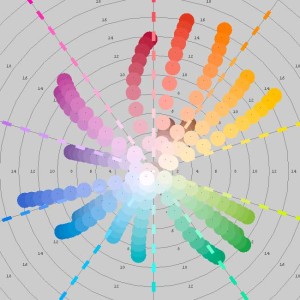
I spent some time examining the characteristics of the WGM mixing method. I found a software program by Zsolt Kovacs-Vajna called rs2color that has a database of reflectance curves of various commercial paints. For example, here are the reflectance curves for 19 of the Liquitex heavy-body acrylic paints:

Reflectance curves for 19 Liquitex HB acrylic paints.

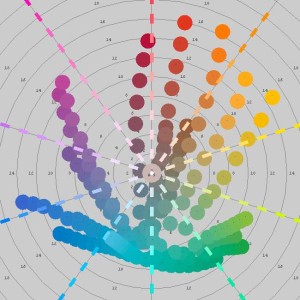
Here are the 19 Liquitex paints plotted on a hue/chroma plane in the rs2color program:

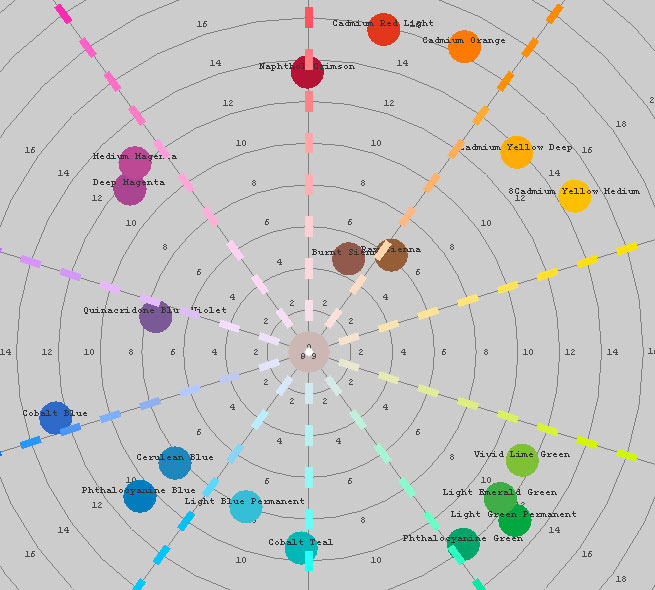
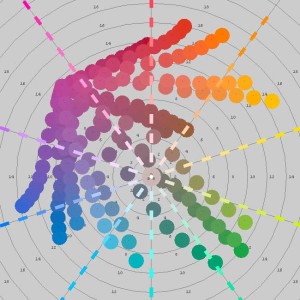
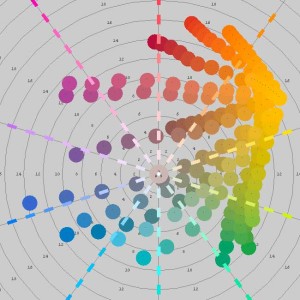
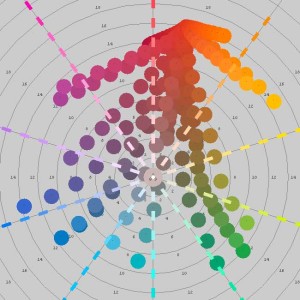
David Briggs examined the mixing of these 19 Liquitex paints, plotting the results in rs2color. He describes how colors that are close to cyan, magenta, and yellow mix well with other colors, giving bright, saturated mixtures. He plots “mixing paths” that show the progression of mixing proportions from 1:0 to 0:1, and describes these paths as an “extroverted octopus” shape, in contrast to the mixing paths he gets when mixing with red, blue, and green, which tend to muddy the mixtures and form an “introverted octopus” shape.

I tried the same thing with the WGM mixing method, generating intermediate mixes 9:1, 8:2, 7:3, … 1:9. The following plots show the mixing curves for six of the Liquitex colors, when mixing them with all the others:

Cyan (#172 Cobalt Teal) mixing with others.

Magenta (#500 Medium Magenta) mixing with others.

Yellow (#830 Cadmium Yellow Medium Hue) mixing with others.

Red (#152 Cadmium Red Light) mixing with others.

Green (#312 Light Green Permanent) mixing with others.

Blue (#381 Cobalt Blue Hue) mixing with others.

It appears that the WGM mixing rule produces very reasonable results! Furthermore, I was pleased to see that some of the “octopus” shapes that David Briggs described are exhibited by the WGM mix, although to a somewhat lesser extent than he observed. I’m not sure what mixing rule is used in rs2color; I’m assuming it is based on a much more advanced theory of paint mixture (such as the Kubelka-Munk theory). In comparison to the rs2color results, it appears that the WGM rule is a promising simplified procedure.

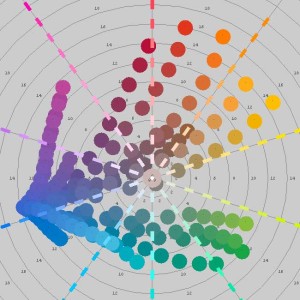
BTW, mixing with black and white also works well. Here are mixing paths for each of the Liquitex colors mixing with:

titanium white (refl = 0.1228, 0.2032, 0.3886, 0.6489, 0.8518, 0.9362, 0.9568, 0.9625, 0.9673, 0.9678, 0.9677, 0.9694, 0.9691, 0.9691, 0.9701, 0.9692, 0.9692, 0.9693, 0.9668, 0.9695, 0.9679, 0.9676, 0.9671, 0.9673, 0.96734, 0.9655, 0.9661, 0.9676, 0.9700, 0.9694, 0.9680, 0.9678, 0.9692, 0.9704, 0.9705, 0.9730)
ivory black (refl = 0.0298, 0.0466, 0.0635, 0.0803, 0.0931, 0.0957, 0.0984, 0.1028, 0.1077, 0.1129, 0.1183, 0.1208, 0.1210, 0.1225, 0.1251, 0.1274, 0.1300, 0.1325, 0.1347, 0.1374, 0.1394, 0.1421, 0.1442, 0.1456, 0.1472, 0.1493, 0.1517, 0.1537, 0.1561, 0.1579, 0.1602, 0.1622, 0.1642, 0.1669, 0.1690, 0.1711)

in intermediate mix ratios of 1:9, 2:8, 3:7, … 9:1

Tints of all colors with titanium white.

Shades of all colors with ivory black.

Be careful not to use zeros for the reflectance curve for black. That represents a colorant with an infinite amount of shading power, which turns the mix black regardless of how little is used!

At this point, you might be wondering, “That’s great, but what about mixing RGB colors instead of reflectance curves?” That is indeed our ultimate goal. I see several approaches we can take to that end.

First, we can look up reflectance curves from RGB values using catalogs of published reflectance curves. This is the easiest approach, but has some pitfalls. We are forced to choose catalog colors that are nearest to our source colors, which may not be near enough for our purposes. Also, this is not a practical solution if we are mixing a large number of colors or if we wish to create a smooth gradient of mixed colors.

The second alternative is to compute a reflectance curve directly from the source sRGB values. This is more complex but appears to be do-able. This is what I consider to be my “original contribution” to this area of study.

Let’s consider the two cases separately in the following sections.

Navigation

The presentation is spread over several web pages. Click the Next Page or Previous Page links to move sequentially. To access a page directly, use these links:

1. Introduction
2. Mathematics of Human Color Perception
3. Subtractive Mixture of Two Reflectance Curves (this page)
4. Cataloged Reflectance Curves
5. Computing Reflectance Curves Directly from sRGB Values

← Previous Page Next Page →