Computing Reflectance Curves Directly from sRGB Values
Instead of relying on existing reflectance measurement data, it is possible to generate reflectance curves directly from sRGB values, and then use these curves in WGM mixing calculations. The main difficulty, however, is that there are an infinite number of different reflectance curves that all give rise to the same color sensation, i.e., the same sRGB color. From a math standpoint, this is evident in the shape of the ![]() matrix; it has many more columns than rows, making the linear system underdetermined.
matrix; it has many more columns than rows, making the linear system underdetermined.
While it is not too difficult to find a single reflectance curve with a specific sRGB value, it may not be suitable for subtractive color mixture computations. For example, a reflectance curve comprising a handful of spiked values at various wavelengths would give awful color mixture results. Or, a reflectance curve with negative values, while mathematically giving the correct sRGB value, would cause WGM calculations to fail completely (raising a negative number to a fractional power is prohibited in real-valued calculations).
I’ve recently developed a set of algorithms that compute reflectance curves from sRGB triplets that give good quality results. By “good quality” I mean they produce reflectance curves quite similar to those of colored objects found in nature, specifically those associated with commercial artist’s paints or color pigments used in those paints. More information can be found at the web page http://scottburns.us/reflectance-curves-from-srgb/, or from the PDF version of the page. There are five algorithms presented on that web page, three of which I recommend for subtractive color mixture computations. Here is a comparison of the three:
| Algorithm Name | Computational Effort | Comments | Link to Matlab Code |
| ILSS (Iterative Least Slope Squared) | Relatively little. | Very fast, but tends to undershoot reflectance curve peaks, especially for bright red and purple colors. Always returns reflectance values in the range 0-1. | link |
| LLSS (Least Log Slope Squared) | About 12 times that of ILSS. | Better quality matches overall, but tends to overshoot peaks in the yellow region. Some reflectance values can be >1, especially for bright red colors. | link |
| ILLSS (Iterative Least Log Slope Squared) | About 20 times that of ILSS. | Best quality matches. Tends to overshoot peaks in the yellow region. Always returns reflectance values in the range 0-1. | link |
UPDATE: I’ve developed a new method, called Least Hyperbolic Tangent Slope Squared (LHTSS), which is as fast as LLSS, guarantees reflectances in the range 0-1, and produces high quality curves that are better than the curves from the slower ILLSS method. This method should be preferred over ILLSS in general.
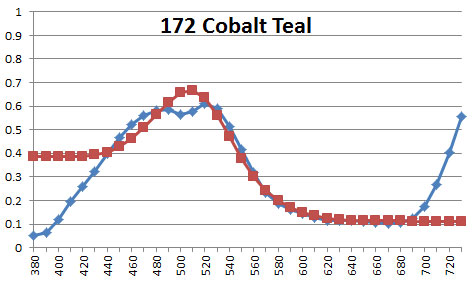
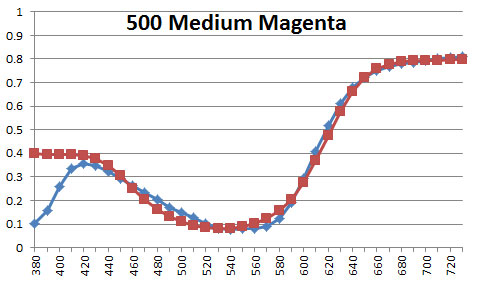
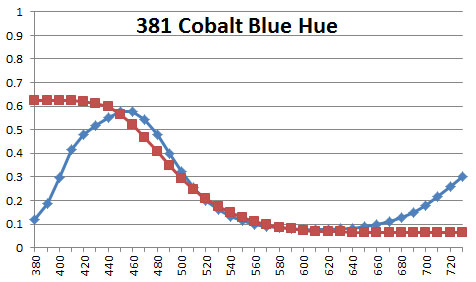
Here are the six Liquitex colors investigated earlier, showing the original measured reflectance (blue curve) and the reflectance generated by the LLSS algorithm (red curve):
Notice how there tends to be more discrepancy between the original reflectance curve and the generated one at the very high and low wavelengths. Human vision is far less sensitive to these outer wavelengths, so these discrepancies have little impact on perceived color. The optimization process takes advantage of this reduced visual sensitivity and keeps the slope as close to zero as possible at both ends of the spectral range. Keep in mind that even though the two curves may differ considerably at the ends, they both give the identical sRGB values and perceived color.
Your choice of which algorithm to use depends on your specific needs. If computational efficiency is more important than realistic color mixing, use ILSS. For best results at the expense of much more computation, use ILLSS. The LLSS method offers a balance of good results and moderately high computational effort.

A comparison of the type of greens that are obtained from mixing yellow and blue in varying proportions by ILSS, LLSS, and ILLSS.
Another factor that may influence the decision of which algorithm to use is one of aesthetics. It is a common expectation that mixing blue and yellow subtractively will give some type of green, instead of the neutral gray that comes from additive color mixture. The difference in the behavior of the various methods has an impact on what kind of green is produced. The figure shows an example of mixing yellow (255,255,0) and blue (0,0,255) in various proportions. It appears that ILLSS and LLSS give brighter and more chromatic greens in comparison to ILSS, which may sway favor toward those methods if the high computational requirements can be tolerated.
Incidentally, if you’re looking for a more powerful green in subtractive mixture, try yellow and cyan instead of yellow and blue!
Other Applications
The work presented here is also applicable to other color spaces, other color matching functions (observers), and other reference illuminants. Recall we started with
![]()
To accommodate other color spaces, the ![]() matrix would be changed. For example, to operate in
matrix would be changed. For example, to operate in ![]() space, simply use the identity matrix for
space, simply use the identity matrix for ![]() . For different RGB color spaces, create a new
. For different RGB color spaces, create a new ![]() matrix from the RGB primaries and reference white according to this calculation. Different standard observers would require different
matrix from the RGB primaries and reference white according to this calculation. Different standard observers would require different ![]() matrices, such as the CIE 1964 10 degree color matching functions. Here is a site compiling many different color matching function sets. Finally, different illuminants would be treated in the computation of
matrices, such as the CIE 1964 10 degree color matching functions. Here is a site compiling many different color matching function sets. Finally, different illuminants would be treated in the computation of ![]() , which is
, which is ![]() . A different illuminant would be implemented by placing it along the diagonal of the
. A different illuminant would be implemented by placing it along the diagonal of the ![]() matrix. The Munsell Color Science Laboratory has links to many different standard illuminants (and a wealth of other data).
matrix. The Munsell Color Science Laboratory has links to many different standard illuminants (and a wealth of other data).
Update 9/26/2018: RGB Components Method
I’ve added a new page that presents an even faster way to generate reflectance curves for subtractive mixture computations. It is as fast as the fastest methods presented on the Generating Reflectance Curves page, guarantees reflectance values in the 0-1 range, but produces reflectance curves that are not as smooth or realistic as the slower, higher quality reconstruction methods. Nevertheless, it permits good quality subtractive mixture with little computational overhead. (This new method is the result of the idea being suggested to me by Brien Dieterle, who asked me to help find a way to implement the idea.)
Update 10/2/2018: Rec 2020 RGB Color Space
I have recently added a new page that shows how to apply these methods to the color space called Recommendation ITU-R BT.2020-2 (10/2015), or Rec. 2020 for short.
Update 2/15/2020: A Word of Caution Regarding RGB Gamut Violations
It has been brought to my attention that when two RGB colors near the outer boundary of the RGB color gamut (near to 0 or 255) are mixed using weighted geometric mean method, the resulting color can sometimes fall slightly outside the 0-1 range. (Thanks to Henry Glick for the heads-up on this!) For example, if we mix red (sRGB=(255,0,0)) and yellow (sRGB=(255,255,0)), we get the following WGM mixture by the various methods:
LLSS: linear rgb of mixture = (0.9133, 0.2052, 0.0089) (within 0-1 gamut)
ILSS: linear rgb of mixture = (1.1093, 0.0474, -0.0271) (out of 0-1 gamut)
ILLSS: linear rgb of mixture = (1.0516, 0.1261, 0.0087) (out of 0-1 gamut)
I’ve performed numerous experiments and have found that all three methods can exceed the 0-1 gamut by up to 8% above 1 and 5% below 0. I recommend that when using WGM to mix colors, to add a step where rgb values outside the 0-1 range are clipped to 0 or 1 before converting to sRGB.
Acknowledgments
I’d like to thank Brad Tober, who approached me a year or so ago about subtractive mixture computation. That prompted me to develop this work, and Brad successfully used the WGM mixing algorithm in one of his projects: Colorigins — a tactile color mixing and matching game. Here is a video showing how it works:
________________________________________

Subtractive Color Mixture Computation by Scott Allen Burns is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Navigation
The presentation is spread over several web pages. Click the Next Page or Previous Page links to move sequentially. To access a page directly, use these links:
1. Introduction
2. Mathematics of Human Color Perception
3. Subtractive Mixture of Two Reflectance Curves
4. Cataloged Reflectance Curves
5. Computing Reflectance Curves Directly from sRGB Values (this page)